Stichprobengröße berechnen für Ihre Online-Umfrage

Eine repräsentative Stichprobe für Ihre Online-Umfrage bekommen Sie, indem Sie die Stichprobengröße im Vorfeld berechnen. Hierfür gibt es eine Formel, die wir Ihnen im Folgenden vorstellen. Wir gehen in einem ersten Schritt auf alle Begriffe der Formel zur Stichprobenberechnung ein und beantworten dann die wichtigsten Fragen: Wie errechnen Sie den optimalen Stichprobenumfang für Ihr aktuelles Umfrageprojekt? Wie viele Personen müssen Sie also befragen, um repräsentative Umfrage-Ergebnisse zu erhalten?

• Wie erhalte ich eine repräsentative Stichprobe für meine Umfrage?
• Berechnung der Stichprobengröße: die Schlüsselbegriffe
• Stichprobengröße errechnen mit einfacher Formel
• Stichprobenumfang berechnen: Beispiel
• Die kleinste sinnvolle Stichprobengröße erhalten
• Berechnung der Stichprobengröße mit Kenntnis der Populationsgröße
• Die häufigsten Fehler bei der Stichprobenberechnung
• Mit Risikofaktoren bei der Stichprobenberechnung umgehen
• Extremfälle der Stichprobenberechnung

Wie erhalte ich eine repräsentative Stichprobe für meine Umfrage?

Berechnung der Stichprobengröße: die Schlüsselbegriffe

Um die folgenden Formeln zur Berechnung der Stichprobengröße zu verstehen, müssen zunächst die wichtigsten Begriffe erläutert werden:

Der Begriff „Population“ (N) bezeichnet die Grundgesamtheit aller Personen, die Sie untersuchen. Wenn es um alle Europäer geht, dann wäre die Population ca. 750 Millionen. Wenn es nur um Raucher in Deutschland geht, wären das ca. 12 Millionen. 

Die Stichprobengröße (n) ist die Anzahl der Personen, welche stellvertretend für die Population befragt werden. Genau diese Größe gilt es zu berechnen – wie viele Personen müssen angesprochen werden, um eine repräsentative Aussage über bspw. die 84 Millionen Einwohner Deutschlands zu erhalten?

Jetzt wird es ein bisschen komplexer: Das Konfidenzniveau gibt an, mit welcher Wahrscheinlichkeit das Ergebnis der Umfrage korrekt ist. Genauer gesagt: mit welcher Wahrscheinlichkeit das Ergebnis innerhalb eines bestimmten Intervalls (Konfidenzintervall) korrekt ist.

Beispiel für das Konfidenzniveau und das Konfidenzintervall: 

1. 1000 Personen werden gefragt, wie hoch die Zustimmung für das politische „Thema A“ in Deutschland ist. 
2. Die Umfrage wird erstellt, durchgeführt und ausgewertet. 
3. Das Ergebnis: 70 % der Befragten (der Probanden) befürworten „Thema A“. 
4. Wir wählen ein Konfidenzniveau von 95%. Das bedeutet, dass wir mit 95%iger Sicherheit sagen möchten, dass der wahre Prozentsatz der Bevölkerung (welche „Thema A“ unterstützen) innerhalb eines bestimmten Intervalls liegt. 
5. Wir berechnen das Konfidenzintervall, zum Beispiel 55% bis 65%. 
6. Ergebnis: wir können mit 95%iger Sicherheit sagen, dass der wahre Prozentsatz der Bevölkerung, der „Thema A“ unterstützt, irgendwo zwischen 55% und 65% liegt.

Zugegeben, wir haben es hier etwas vereinfacht – in Punkt 5. sagen wir schlicht „Wir berechnen das Konfidenzintervall“. Das Konfidenzintervall ist letztendlich die +/- Fehlerspanne (E), in welcher sich der tatsächliche Wert befindet. Also die Fehlerspanne, die sich ergibt, da wir nicht die gesamte Population befragen.

Was bedeutet das für unseren Fall der Stichprobenerrechnung? Wir müssen beide Größen – Konfidenzniveau und Konfidenzintervall (Fehlerspanne) – im Vorfeld festlegen: Wir nehmen uns vor, dass wir ein Ergebnis anstreben, bei welchem wir mit (Konfidenz) 95%iger Sicherheit sagen können, dass unser Ergebnis zwar nicht exakt ist, aber höchstens um +/- 3% (Fehlerspanne / Konfidenzintervall) von der Realität abweicht.

Ein weiterer Schlüsselbegriff ist (p), der Anteil des Merkmals in der Grundgesamtheit. (p) ist eine Größe in Prozent, jedoch ausgedrückt in Dezimalzahlen. Dieser kann zwischen 0 und 100% variieren. Der Wert kann bekannt, unbekannt und mehr oder weniger einfach ermittelbar sein. Angenommen Sie untersuchen die Raucher einer Stadt. Da Sie nicht wissen, wie hoch deren Anteil ist, können Sie eine Umfrage vorab durchführen. Danach können Sie mit dem Ergebnis die notwendige Stichprobe ermitteln. Oder Sie machen es sich einfach: Sie nutzen den Wert 0,5. Das ist die konservativste Lösung, da (p) in der Stichprobenformel mit p*(1-p) eingesetzt wird und somit bei 0,5 das Maximum erreicht. Sie berechnen zwar eine (unnötig) hohe Stichprobengröße, sind aber auf der sicheren Seite.

Z-Wert: Zur Berechnung der Stichprobengröße wird zuletzt auch der Z-Wert benötigt. Der Z-Wert ist, salopp formuliert, die Standardabweichung, gemessen in Standardabweichungen. Mit diesem Wert wird bestimmt, wie weit ein bestimmter Wert von einem Durchschnitt entfernt ist, gemessen in Standardabweichungen. Er hilft uns zu verstehen, wie außergewöhnlich ein bestimmter Wert im Vergleich zum Durchschnitt ist und wie sicher wir uns über unsere Schlussfolgerungen sein können. Die gute Neuigkeit: Sie brauchen den Z-Wert nicht zu berechnen, sondern können diesen aus der Z-Wert-Tabelle (bzw. Z-Score-Tabelle) auslesen. Anbei die Z-Werte für die am häufigsten genutzten Konfidenzniveaus:

Gewünschtes Konfidenzniveau Z-Wert

90 % 1,65

95 % 1,96

99 % 2,58 

Stichprobengröße errechnen mit einfacher Formel

Sie können die optimale Stichprobengröße errechnen ohne Berücksichtigung und Kenntnis der Populationsgröße – mit einer einfachen Formel. Wie oben beschrieben, brauchen wir hierfür unterschiedliche Variablen, die jedoch alle vorab festgelegt oder sehr sicher geschätzt, berechnet oder einer Tabelle entnommen werden können.

• Der Z-Wert wird aus der Z-Wert-Tabelle ausgelesen
• P wird konservativ auf 0,5 festgelegt
• Die Fehlerspanne und das Konfidenzniveau werden festgelegt

Zusammengesetzt ergibt sich dann die Formel:

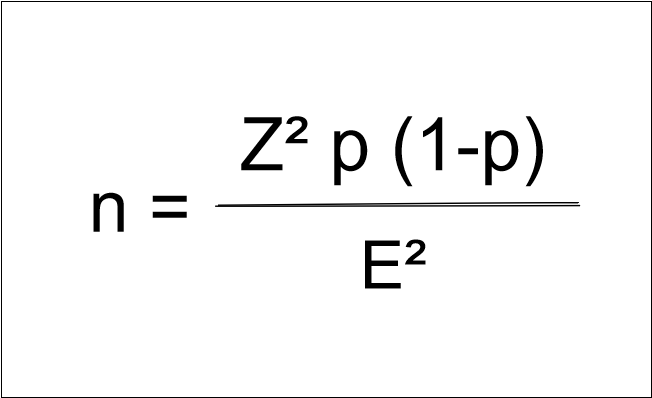Abb. 1- Formel für die Stichprobenberechnung

Beziehungsweise, da wir ja p = 0,5 rechnen und somit p(1-p) = 0,25 ergibt, gilt folgende Formel für unbekannte Populationsverteilungen:

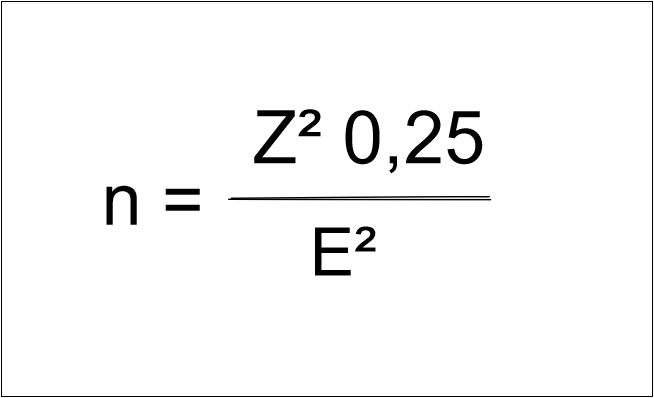Abb.2 - Formel für die Stichprobenberechnung mit p= 0,5 

Stichprobenumfang errechnen: Beispiel

Wie man den Stichprobenumfang errechnet, lässt sich an einem konkreten Beispiel noch deutlicher machen: Wir möchten eine Umfrage zur Erfassung des Rauchverhaltens in Deutschland durchführen und möchten den Stichprobenumfang basierend auf bestimmten Annahmen berechnen.

Wir möchten eine 95%ige Konfidenz (entspricht einem Z-Wert von 1,96, siehe Tabelle oben) und einen Fehlerschätzwert (E) von 3% (0,03) verwenden. Der aktuelle Anteil der Raucher in Deutschland beträgt ca. 24% (p). 

Wir berechnen:

n = (1,96^2 * 0,24 * (1-0,24)) / (0,03^2)

n ~ 779

Wir müssten also ca. 779 Personen befragen.

Wenn wir den Anteil der Raucher nicht kennen würden und für p den konservativen, maximalen Wert 0,5 einsetzen, kämen wir auf eine größere notwendige Stichprobe, auf 1068 Personen. 

Die kleinste sinnvolle Stichprobengröße erhalten

Das obige Beispiel zeigt, dass weitaus mehr mehr Teilnehmer befragt werden müssen, weil wir die Verteilung nicht kennen. Es ist jedoch entweder sehr aufwendig, repräsentative (und willige) Teilnehmer zu rekrutieren, oder sehr teuer (Online Panels). Insofern ergibt es natürlich Sinn, die kleinste sinnvolle Stichprobe einzusetzen. Die Stellhebel hierfür sind die Formelbestandteile:

• Die Konfidenz: je niedriger, desto weniger Teilnehmer werden benötigt
• Die Fehlerspanne: je niedriger, desto mehr Teilnehmer sind zu rekrutieren
• Die Verteilung: je weiter weg von der 0,5 (also näher an 0 oder an der 1), desto weniger Teilnehmer / kleiner die Stichprobe

Das Konfidenzniveau und die Fehlerspanne können frei festgesetzt werden. Hier geht es vor allem darum, wie exakt Ihre Projektergebnisse sein müssen. Das kann auch vorgegeben sein. Doch bei der Verteilung gibt es mehr Spielraum: bei unbekannter Verteilung macht oftmals eine Umfrage vorab Sinn. Im obigen Beispiel wäre es ratsam, eine repräsentative Umfrage vorab durchzuführen, um den Anteil der Raucher vorab zu ermitteln.

Berechnung der Stichprobengröße mit Kenntnis der Populationsgröße

Die Stichprobengröße kann natürlich auch berechnet werden, wenn die Populationsgröße (N) bekannt ist. Hierfür gibt es eine erweiterte Formel:

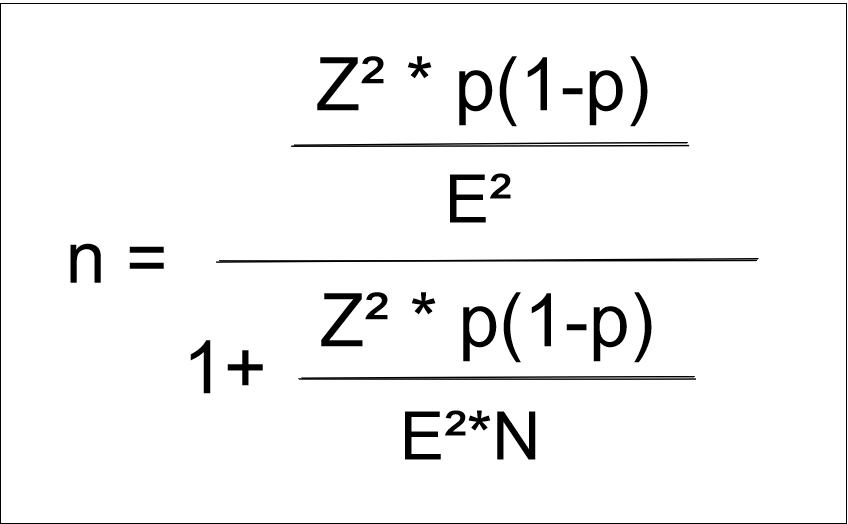Abb. 3- Erweiterte Formel zur Stichprobenberechnung mit bekannter Populationsgröße

Beispiel für die Errechnung der Stichprobengröße mit Kenntnis der Population (N):

Rahmendaten: 5000 Mitarbeiter, gewünschtes Konfidenzniveau: 95%, Fehlerspanne: 5% und unbekannter Anteil des Merkmals in der Bevölkerung:
N = 5000
Z = 1,96 (entspricht einem Konfidenzniveau von 95%)
p = 0,5
E = 0,05 (Präzision von ±5%)

Wir berechnen dann:
n = (5000 * 1,96^2 * 0,5 * (1 - 0,5)) / ((5000 - 1) * 0,05^2 + 1,96^2 * 0,5 * (1 - 0,5))
n = (5000 * 3,8416 * 0,25) / (4999 * 0,0025 + 3,8416 * 0,25)
n = 480,2

Übrigens: Wenn Sie die optimale Stichprobengröße für Ihr Umfrageprojekt berechnet haben, dann geht es in einem folgenden Schritt an die Einladung der Umfrageteilnehmer zu Ihrer Umfrage. Unser Tool bietet hierfür verschiedene Möglichkeiten. Lesen Sie zu diesem Thema gern in unserem Helpdesk weiter: Einladung zur Umfrage

Die häufigsten Fehler bei der Stichprobenberechnung

Bei der Stichprobenberechnung können verschiedene Fehler gemacht werden. Wir nennen Ihnen im Folgenden die 6 häufigsten Fehler, die Sie bei der Errechnung Ihrer Stichprobengröße für Ihr Umfrageprojekt unbedingt vermeiden sollten.

1. Unzureichende Stichprobengröße: Eine zu kleine Stichprobe kann zu ungenauen oder nicht repräsentativen Ergebnissen führen. Bei kleiner Population (bspw. unter 100) empfiehlt sich eine Vollerhebung.
2. Auswahlbias: Wenn die Stichprobe nicht zufällig ausgewählt wird, sondern bestimmte Gruppen bevorzugt oder benachteiligt werden, kann dies zu Verzerrungen führen.
3. Nichtrepräsentative Stichprobe: Wenn die Stichprobe nicht die gesamte Population gut widerspiegelt, können die Ergebnisse nicht verallgemeinert werden.
4. Selbstselektion: Wenn die Teilnahme an der Stichprobe auf freiwilliger Basis erfolgt, können Personen mit bestimmten Eigenschaften eher teilnehmen, was zu Verzerrungen führen kann.
5. Ausreißer: Einzelne extreme Werte in der Stichprobe können das Ergebnis stark beeinflussen, wenn sie nicht angemessen behandelt werden.

Mit Risikofaktoren bei der Stichprobenberechnung umgehen

Um die Fehler bei der Stichprobenberechnung zu verhindern oder abzuschwächen, können verschiedene Maßnahmen ergriffen werden:

1. Unzureichende Stichprobengröße: Durch eine Berechnung der erforderlichen Stichprobengröße vor der Datenerhebung kann sichergestellt werden, dass genügend Datenpunkte vorhanden sind, um aussagekräftige Ergebnisse zu erzielen. Darum auch vorliegende Hilfestellung, um die Stichprobengröße nicht nach „Bauchgefühl“ oder „gesundem Menschenverstand“ auszuwählen, sondern mathematisch korrekt. Es ist wichtig, statistische Methoden zur Bestimmung der Stichprobengröße zu verwenden, basierend auf dem gewünschten Konfidenzniveau, der erwarteten Varianz und dem erwarteten Effekt.
2. Auswahlbias: Um einen Auswahlbias zu vermeiden, sollte eine Zufallsstichprobe gezogen werden. Dies kann durch randomisierte Stichprobenziehungstechniken wie einfache Zufallsstichprobe, stratifizierte Zufallsstichprobe oder geschichtete Zufallsstichprobe erreicht werden. Dadurch wird sichergestellt, dass jede Einheit der Population eine gleiche Chance hat, in die Stichprobe aufgenommen zu werden. Gleiches gilt für die nichtrepräsentative Stichprobe.
3. Selbstselektion: Wenn Selbstselektion ein Problem darstellt, sollten geeignete Maßnahmen ergriffen werden, um die Teilnahmebereitschaft zu erhöhen und eine breitere Teilnahmebasis zu erreichen. Dies kann beispielsweise durch Anreize für die Teilnahme und sorgfältige Kommunikation über unterschiedliche Kanäle erreicht werden.
4. Ausreißer: Bei der Behandlung von Ausreißern ist es wichtig, zwischen echten Ausreißern (also tatsächlich ungewöhnlichen Werten) und Messfehlern zu unterscheiden. Es können robuste statistische Methoden verwendet werden, die weniger empfindlich gegenüber Ausreißern sind, oder Ausreißer können vor der Analyse überprüft und gegebenenfalls korrigiert werden.

Es ist wichtig, dass Umfrageersteller bei der Stichprobenberechnung und -auswahl sorgfältig vorgehen und die geeigneten Methoden und Verfahren basierend auf den spezifischen Anforderungen und Bedingungen ihrer Studie wählen.

Extremfälle der Stichprobenberechnung

Eine Stichprobe = 1 reicht manchmal vollkommen aus: Sie kochen eine Suppe und möchten wissen, ob Pfeffer fehlt: Sie müssen natürlich nicht den ganzen Topf auslöffeln. Ein kleines Löffelchen reicht. Denn Sie haben die Suppe ordentlich umgerührt und das Merkmal „Pfeffergehalt“ ist überall gleich. In der Marktforschung würde man sagen: Im Extremfall einer Varianz von Null reicht eine Stichprobe von n=1. Es gilt also, wenn alle Datenpunkte den gleichen Wert haben, dann reicht eine Stichprobe von n=1 aus: Sie fragen auch nur eine Person, welches Datum wir heute haben.

Zurück zur Suppe: Stellen Sie sich vor, Sie haben kurz geträumt. Sie richten Ihren Blick auf die Suppe, haben den Salzsteuer in der Hand. Sie haben noch nicht umgerührt, aber haben Sie bereits gesalzen? Wie viele Löffel müssten Sie nun probieren, um mit einer hinreichend hohen Wahrscheinlichkeit sagen zu können, ob Salz drin ist? Wenn Sie nicht alles inklusive des allerletzten Löffels aufessen, können Sie auch nicht zu 100% sagen, ob die Suppe gesalzen ist. Die Suppe aufzuessen wäre zwar effektiv, aber alles andere als effizient... Jetzt kommt die Wahrscheinlichkeitsrechnung ins Spiel, Sie wenden obengenannte Formel an, teilen die Suppe gedanklich in X Löffelchen, freunden sich mit einer Wahrscheinlichkeit von 99% an und legen los...

Jetzt Online Umfrage erstellen